Guided Quantum Walk (Best Poster Finalist)
Monday, May 13, 2024 3:00 PM to Wednesday, May 15, 2024 4:00 PM · 2 days 1 hr. (Europe/Berlin)
Foyer D-G - 2nd floor
Research Poster
Integration of Quantum Computing and HPCQuantum Computing - Basics and TheoryQuantum-inspired Algorithms and Technologies
Information
Poster is on display and will be presented at the poster pitch session.
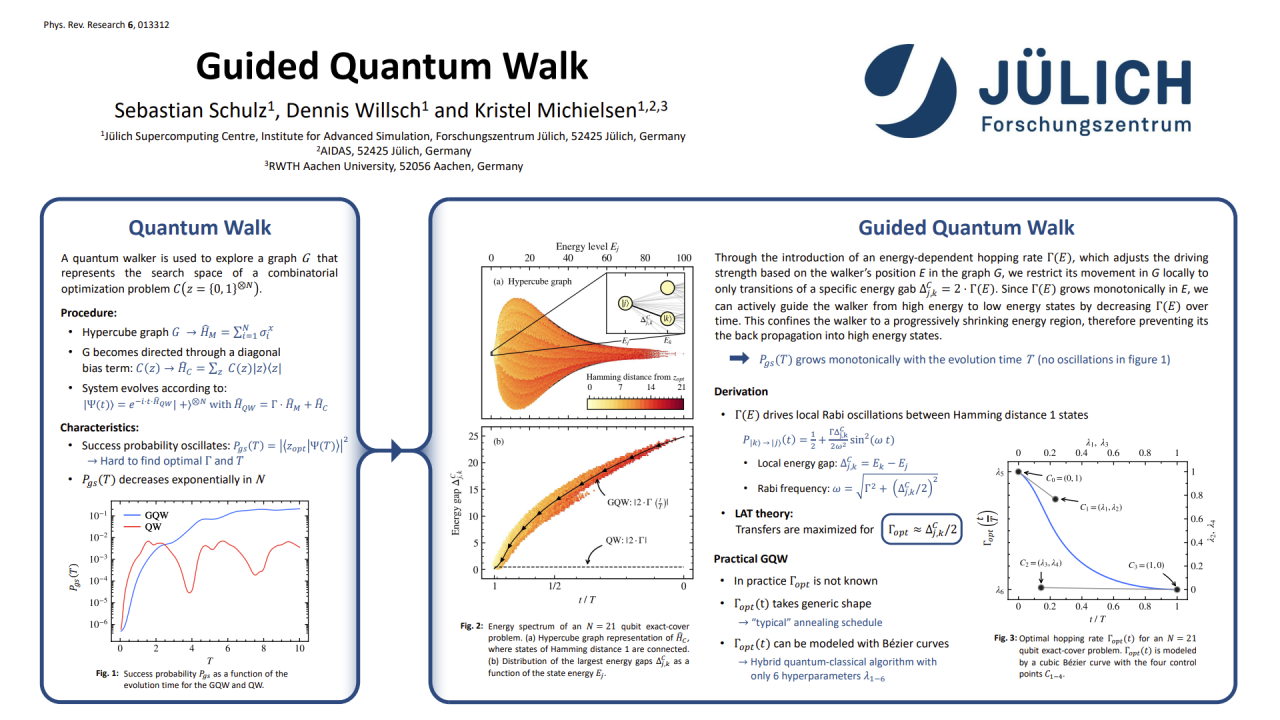
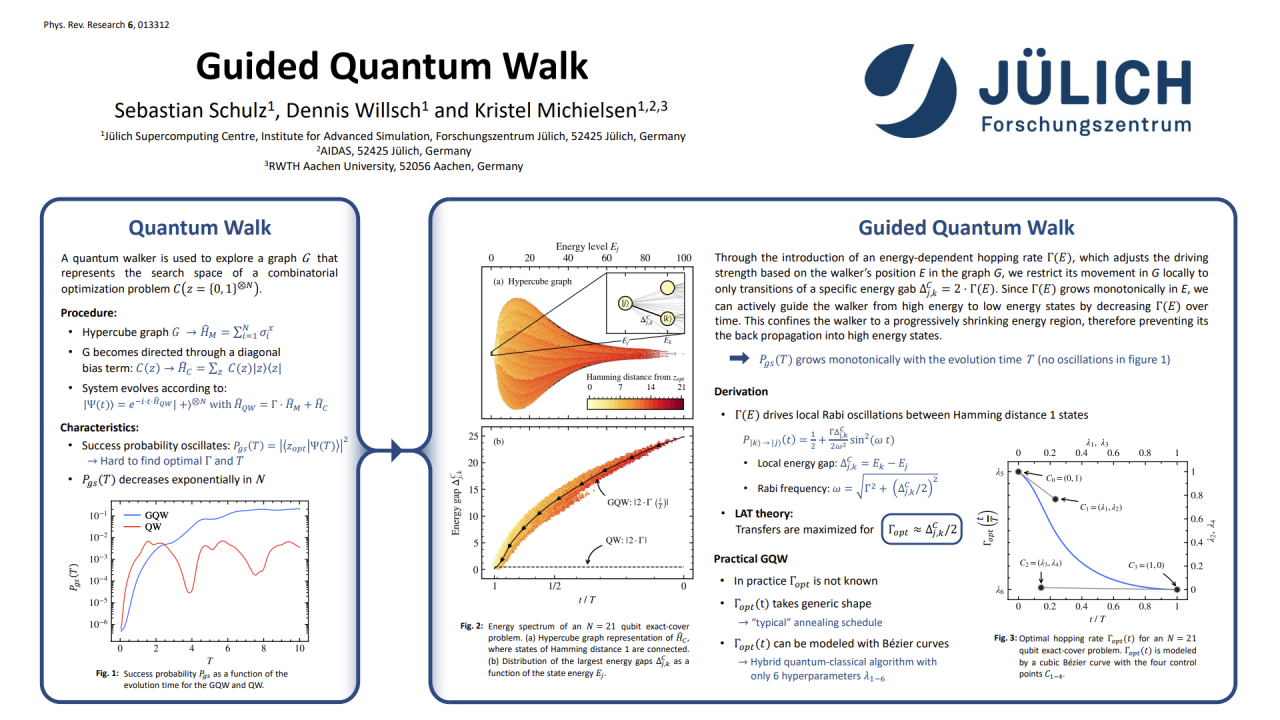
Quantum algorithms, such as quantum walks (QWs) and quantum annealing (QA), have generated significant attention for their potential to solve large-scale combinatorial optimization problems. In this research, we utilize the theory of local amplitude transfer (LAT) to delve into the operational principles of these algorithms beyond the adiabatic theorem, providing insights into the design of optimal quantum evolutions. By representing the eigenspace of the problem Hamiltonian as a hypercube graph, we demonstrate that probability amplitude traverses the search space through a series of local Rabi oscillations. We argue that the amplitude movement can be systematically guided towards the ground state using a time-dependent hopping rate based solely on the problem’s energy spectrum. Building upon these insights, we extend the concept of multistage QW by introducing the guided quantum walk (GQW) as a bridge between QW-like and QA-like procedures. We assess the performance of the GQW on exact cover and garden optimization problems with 12 to 40 qubits. Our results provide evidence for the existence of optimal annealing schedules, beyond the requirement of adiabatic time evolutions. These schedules might be capable of solving large-scale combinatorial optimization problems within evolution times that scale linearly in the problem size.
Contributors:
Quantum algorithms, such as quantum walks (QWs) and quantum annealing (QA), have generated significant attention for their potential to solve large-scale combinatorial optimization problems. In this research, we utilize the theory of local amplitude transfer (LAT) to delve into the operational principles of these algorithms beyond the adiabatic theorem, providing insights into the design of optimal quantum evolutions. By representing the eigenspace of the problem Hamiltonian as a hypercube graph, we demonstrate that probability amplitude traverses the search space through a series of local Rabi oscillations. We argue that the amplitude movement can be systematically guided towards the ground state using a time-dependent hopping rate based solely on the problem’s energy spectrum. Building upon these insights, we extend the concept of multistage QW by introducing the guided quantum walk (GQW) as a bridge between QW-like and QA-like procedures. We assess the performance of the GQW on exact cover and garden optimization problems with 12 to 40 qubits. Our results provide evidence for the existence of optimal annealing schedules, beyond the requirement of adiabatic time evolutions. These schedules might be capable of solving large-scale combinatorial optimization problems within evolution times that scale linearly in the problem size.
Contributors:
Format
On-site

