Task Parallelization for Sparse Direct Solver with Mixed Precision Arithmetic
Monday, May 13, 2024 3:00 PM to Wednesday, May 15, 2024 4:00 PM · 2 days 1 hr. (Europe/Berlin)
Foyer D-G - 2nd floor
Research Poster
Mixed PrecisionNovel Algorithms
Information
Poster is on display and will be presented at the poster pitch session.
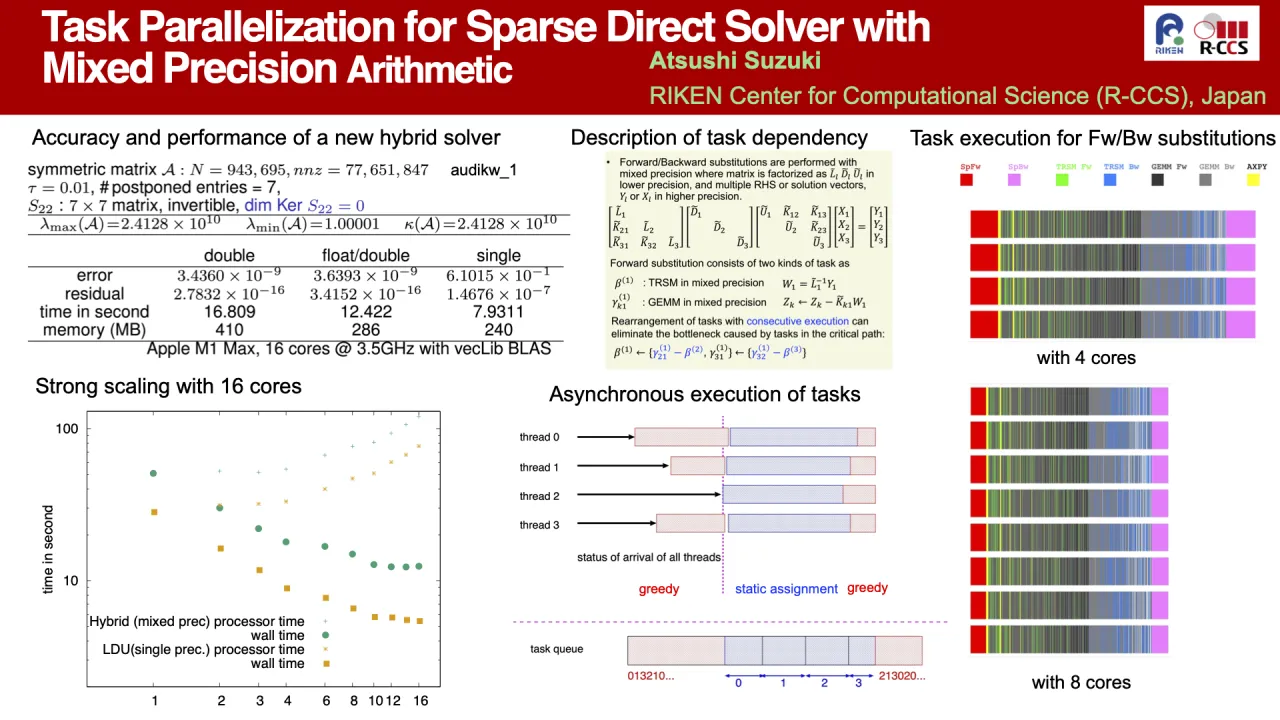
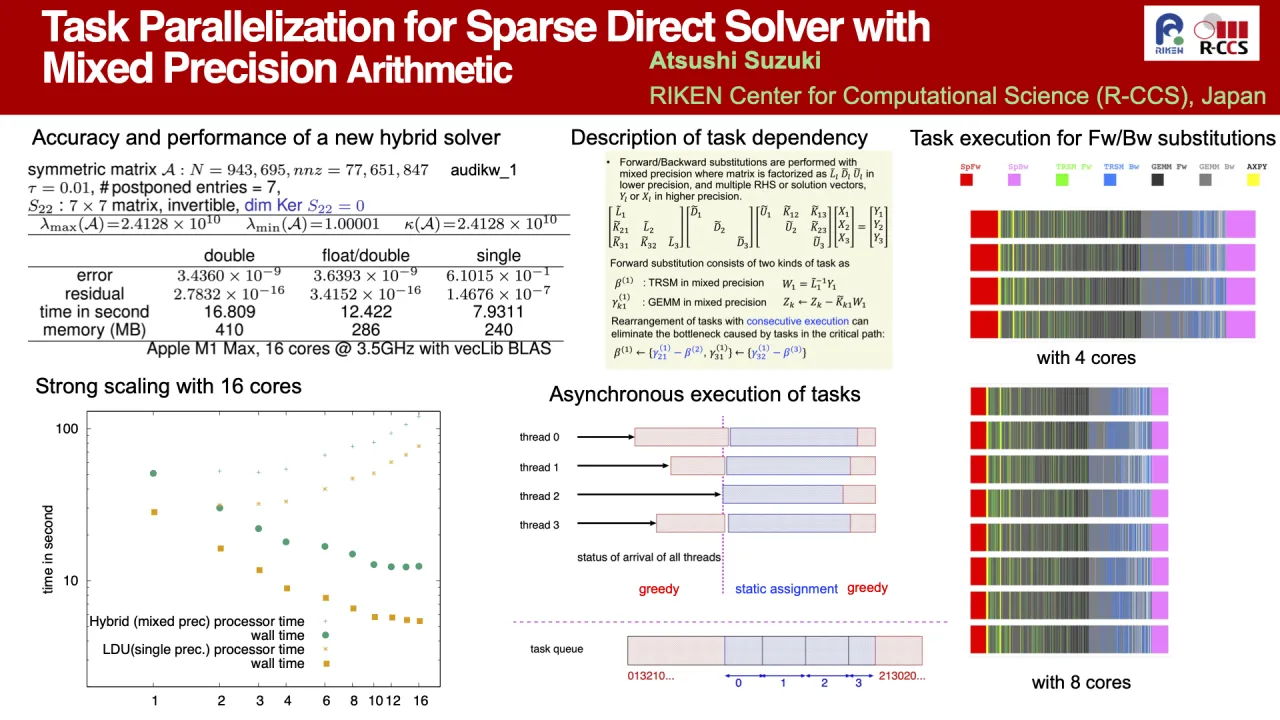
LDU-factorization with pivoting strategy provides robust solver for sparse matrices with large condition number. However, computational complexity of the factorization solver is high and this complexity of number of unknowns cannot be reduced, but by using lower precision arithmetic, computational cost and memory usage could be reduced. Nested-dissection ordering provides multi-frontal factorization and threshold pivoting for each sub-matrix can extract a set of sub-matrices with moderate condition number. This factorization procedure leads to a hybrid algorithm that consists of three phases: 1. factorization with threshold pivoting in lower precision to identify moderate part, 2. generation of the Schur complement in higher precision by iterative solver using factorized matrix in lower precision as a preconditioner, and 3. factorization with full pivoting and kernel detection in higher precision. For the preconditioner, actual mixed precision arithmetic is used in forward/backward substitution procedure with factorized matrix in lower precision and RHS vectors in higher precision. Here main operations consist of BLAS level 3 routines, TRSM and GEMM, which run on a single core within task runtime instead of usage of threaded version of BLAS. Task description for factorization consists of homogeneous precision due to lower precision arithmetic for moderate part of the matrix, but one for forward/backward substitution consists of mixed precision with working arrays to keep internal operations, which is written by C++ template in generic programming manner. Preliminary result is obtained by tmBLAS implementation for mixed precision and by own runtime using C++ thread class, which shows strong scalability with 16 cores.
LDU-factorization with pivoting strategy provides robust solver for sparse matrices with large condition number. However, computational complexity of the factorization solver is high and this complexity of number of unknowns cannot be reduced, but by using lower precision arithmetic, computational cost and memory usage could be reduced. Nested-dissection ordering provides multi-frontal factorization and threshold pivoting for each sub-matrix can extract a set of sub-matrices with moderate condition number. This factorization procedure leads to a hybrid algorithm that consists of three phases: 1. factorization with threshold pivoting in lower precision to identify moderate part, 2. generation of the Schur complement in higher precision by iterative solver using factorized matrix in lower precision as a preconditioner, and 3. factorization with full pivoting and kernel detection in higher precision. For the preconditioner, actual mixed precision arithmetic is used in forward/backward substitution procedure with factorized matrix in lower precision and RHS vectors in higher precision. Here main operations consist of BLAS level 3 routines, TRSM and GEMM, which run on a single core within task runtime instead of usage of threaded version of BLAS. Task description for factorization consists of homogeneous precision due to lower precision arithmetic for moderate part of the matrix, but one for forward/backward substitution consists of mixed precision with working arrays to keep internal operations, which is written by C++ template in generic programming manner. Preliminary result is obtained by tmBLAS implementation for mixed precision and by own runtime using C++ thread class, which shows strong scalability with 16 cores.
Format
On-site

